
Όλοι γνωρίζουμε πως η Γη είναι περίπου σφαιρική. Έχεις αναρωτηθεί ποτέ όμως γιατί είναι σφαιρική; Γιατί δεν είναι κυβική ή κυλινδρική ή (τυχαίο παράδειγμα) επίπεδη;
Θα μπορούσαμε να γενικεύσουμε την ερώτηση και να την κάνουμε «Γιατί όλοι οι πλανήτες είναι σφαιρικοί;». Αυτό όμως θα ήταν ελαφρώς παραπλανητικό γιατί ένας πλανήτης είναι εξ’ ορισμού σφαιρικός.
Το 2006 η Διεθνής Αστρονομική Ένωση έθεσε τρία κριτήρια που πρέπει να πληροί ένα ουράνιο σώμα για να ονομάζεται πλανήτης:
1. Πρέπει να βρίσκεται σε τροχιά γύρω από τον Ήλιο,
2. Πρέπει να έχει καθαρίσει τη γειτονική του περιοχή από άλλα συγκρίσιμου μεγέθους σώματα – εκτός από τους δορυφόρους του – και
3. Πρέπει να έχει επαρκή μάζα ώστε να έχει στρογγυλοποιηθεί κάτω από την επίδραση της βαρύτητάς του. 1
Ο ορισμός αυτός έχει κάποια προβλήματα και είναι ένα αμφιλεγόμενο θέμα ανάμεσα στους αστρονόμους, αλλά εγώ θέλω να σταθώ στο κριτήριο 3, το οποίο εξηγεί γιατί ορισμένα ουράνια σώματα, όπως οι πλανήτες, έχουν σφαιρικό σχήμα ενώ άλλα, όπως οι αστεροειδείς, έχουν ακανόνιστο.
Όπως μαρτυράει το κριτήριο, ο κύριος λόγος είναι η βαρύτητα.
Φαντάσου πως έχεις ένα δοχείο με νερό και ένα τοίχωμα τοποθετημένο όπως στην εικόνα.

Αν αφαιρέσεις το τοίχωμα, το νερό θα μετακινηθεί προς τα δεξιά μέχρι να δημιουργήσει μια επίπεδη επιφάνεια. Αυτό συμβαίνει γιατί το νερό κινείται προς τα κάτω και σταματάει μόνο όταν δεν υπάρχει άλλος τρόπος για να συνεχίσει. Όταν βέβαια λέμε «κάτω», εννοούμε προς την κατεύθυνση της βαρύτητας. Μπορούμε να θεωρήσουμε τη βαρύτητα της Γης σαν μια δύναμη που τραβάει όλα τα σώματα προς το κέντρο της. Άρα το νερό κινείται προς τα κάτω έτσι ώστε να απέχει τη μικρότερη δυνατή απόσταση από το κέντρο της Γης.
Για ένα μικρό δοχείο η κατεύθυνση «κάτω» είναι παντού η ίδια. Για έναν πλανήτη όμως, ή έναν αστέρα, εξαρτάται από το που βρίσκεσαι: Το «κάτω» στον Βόρειο Πόλο είναι διαφορετικό από το «κάτω» στον Ισημερινό.
Ας φανταστούμε τώρα έναν τεράστιο, κυβικό, υδάτινο πλανήτη. Για κάθε σημείο του πλανήτη το «κάτω» είναι η κατεύθυνση προς το κέντρο του. Κάποια σημεία όμως απέχουν από το κέντρο περισσότερο από κάποια άλλα.

Όπως ακριβώς στο προηγούμενο παράδειγμα, το νερό στον υποθετικό, κυβικό μας πλανήτη θα κινηθεί προς τα «κάτω» μέχρις ότου όλα τα μόρια στην επιφάνεια να απέχουν την ίδια απόσταση από το κέντρο του. Αλλά αυτός ακριβώς είναι ο ορισμός της σφαίρας.

Το νερό όμως είναι ρευστό και μπορεί να ρέει. Πώς απέκτησε σφαιρικό σχήμα ένας πετρώδης πλανήτης σαν τη Γη;
Tο σχήμα τον πλανητών καθορίζεται κατά τα πρώτα χρόνια σχηματισμού τους, όπου τα πάντα είναι λίγο πιο ζεστά, λίγο πιο ρευστά και λίγο πιο τρομακτικά. Επίσης, στη γεωλογική κλίμακα των εκατομμυρίων και δισεκατομμυρίων ετών, ακόμη και τα στερεά, μέσα από τη συνεχή επίδραση της βαρύτητας, συμπεριφέρονται κατά προσέγγιση σαν ρευστά.
Παρ’ όλα αυτά, η Γη δεν είναι απολύτως λεία. Έχει κορυφές και κοιλάδες. Η βαρύτητα της δεν είναι ανίκητη – οι χημικοί δεσμοί των στερεών αντικειμένων είναι αρκετά δυνατοί. Τα βουνά της Γης μπορούν να υψώνονται ενάντια στη δύναμη της βαρύτητας λόγω της ανθεκτικότητας των βράχων. Το Έβερεστ απέχει περίπου 9 χιλιόμετρα από την επιφάνεια της θάλασσας, αλλά ακόμη και αυτή η απόσταση είναι ένα μικροσκοπικό κλάσμα της ακτίνας της Γης.

Η Γη είναι πολύ πιο λεία απ’ όσο νομίζουμε. Αν μπορούσαμε να τη σμικρύνουμε ώστε να την κρατήσουμε στο χέρι μας θα ήταν πιο λεία και από μία μπάλα μπιλιάρδου!
Ακόμα και τα ψηλότερα βουνά της Γης όμως φαίνονται σαν λόφοι μπροστά σε άλλα βουνά του ηλιακού συστήματος. Για παράδειγμα, το όρος Όλυμπος στον Άρη, είναι το υψηλότερο βουνό-ηφαίστειο στο ηλιακό σύστημα και έχει ύψος περίπου 25 χιλιόμετρα! Η συνταγή είναι αρκετά απλή: Όσο πιο ασθενής είναι η βαρύτητα σε ένα ουράνιο σώμα, τόσο πιο ψηλά μπορούν να φτάσουν τα βουνά του. Το Έβερεστ είναι περίπου όσο ψηλό θα μπορούσε να είναι ένα βουνό στη Γη προτού τα χαμηλότερα στρώματα υποκύψουν στην ίδια τους την πλαστικότητα κάτω από το βάρος των υπόλοιπων.
Δεν έχουν όμως όλα τα ουράνια σώματα το ίδιο σχήμα γιατί ορισμένα δεν είχαν επαρκή μάζα ώστε η βαρύτητα να τα μετατρέψει σε σφαίρες. Στην ακτίνα που ένα σώμα πρέπει να έχει για να είναι σφαιρικό, δόθηκε από δύο Αυστραλούς ερευνητές το εμπνευσμένο όνομα «ακτίνα της πατάτας». Η ακτίνα της πατάτας για βραχώδη σώματα είναι περίπου 300 χιλιόμετρα, ενώ για σώματα που αποτελούνται κυρίως από πάγο είναι περίπου 200 χιλιόμετρα. Ο πάγος έχει πιο αδύναμους χημικούς δεσμούς από την πέτρα, έτσι κάνει το έργο της βαρύτητας ευκολότερο. 2

(Παράγωγη εικόνα από την αρχική του Jono Hey - sketchplanations.com)
Αν ένα σώμα έχει ακτίνα μικρότερη από 200 χιλιόμετρα τότε είναι δυνατό σχεδόν οποιοδήποτε σχήμα, όπως μπορούμε να δούμε από τους πάρα πολλούς αστεροειδείς στο ηλιακό μας σύστημα. Κλασικά παραδείγματα είναι ο Φόβος και ο Δείμος, οι δύο δορυφόροι του Άρη, με μέση ακτίνα 11 και 6 χιλιόμετρα αντίστοιχα.

Εκτός απ’ τη βαρύτητα, πολύ σημαντικό ρόλο στο σχήμα ενός σώματος παίζει και η ταχύτητα περιστροφής του. Κανένα ουράνιο σώμα δεν είναι απόλυτα σφαιρικό γιατί όλα τα ουράνια σώματα περιστρέφονται.
Ένα σώμα που περιστρέφεται γίνεται πεπλατυσμένο στους πόλους του, με την πεπλάτυνση να εξαρτάται από την ταχύτητα περιστροφής. Στην παρακάτω εικόνα η διακεκομμένη κόκκινη γραμμή σχηματίζει έναν τέλειο κύκλο. Ο Κρόνος επειδή περιστρέφεται πιο γρήγορα είναι πιο πεπλατυσμένος από τη Γη.

Και αυτή εδώ είναι η Χαουμέια, ένας νάνος πλανήτης, που έχει πάρει αυτό το σχήμα κυρίως γιατί περιστρέφεται πιο γρήγορα, απ’ όσο γνωρίζουμε, από οποιοδήποτε άλλο σώμα στο ηλιακό σύστημα.

Θα μπορούσε άραγε ένας πλανήτης να περιστρέφεται τόσο γρήγορα ώστε να είναι επίπεδος; Όσο πιο γρήγορα περιστρέφεται, τόσο μεγαλύτερη φυγόκεντρη δύναμη δέχεται η επιφάνειά του. Αν αυτή η δύναμη γίνει μεγαλύτερη της βαρύτητας, τότε ο πλανήτης θα αρχίσει να εκσφενδονίζει τα κομμάτια του στο διάστημα, όπως ένας σκύλος τινάζει το νερό από πάνω του.
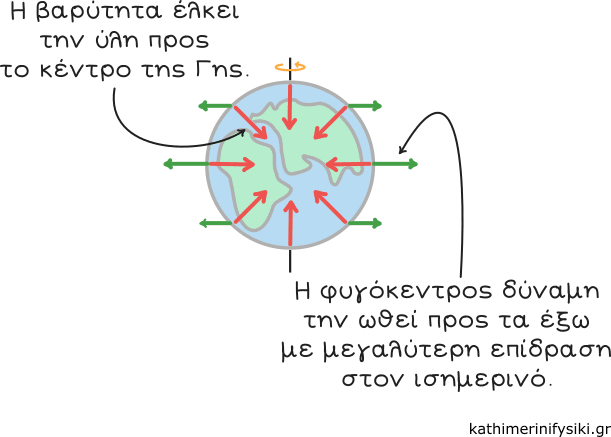
Υπάρχει έτσι ένα πρακτικό όριο στην ταχύτητα περιστροφής. Η Γη, για παράδειγμα, θα μπορούσε ίσως να αποκτήσει ένα ελλειψοειδές σχήμα με λόγο ακτίνων 3:1 πριν αρχίσει να διαλύεται. Αυτό είναι όσο πιο κοντά σε επίπεδη Γη η φυσική επιτρέπει να φτάσουμε. 3
Αν τώρα, κάπου στο αχανές σύμπαν, υπάρχει κάποιος πλανήτης που αντέχει σε μεγαλύτερες ταχύτητες περιστροφής, θεωρητικά θα μπορούσε να λάβει περισσότερα σχήματα. Από σφαιρικός, όταν είναι ακίνητος, σε ελλειψοειδής και έπειτα σε σχήμα με δύο, τρεις και τέσσερις λοβούς. 4
Επίσης θεωρητικά εφικτός, είναι και ένας… τόρος! Ακούγεται πιο τρελό και από μια επίπεδη Γη, αλλά ένας τοροειδής πλανήτης δεν απαγορεύεται από τους νόμους της φυσικής. Απλά είναι μάλλον ακατόρθωτο να σχηματιστεί φυσικά. Αν ωστόσο κάποιος τον δημιουργούσε, ίσως κάποιος εξωγήινος πολιτισμός με περίεργες ορέξεις, θα μπορούσε θεωρητικά να παραμείνει σταθερός. 5
Σε έναν τέτοιον πλανήτη, τα κουλούρια θα είναι τοροειδή ή σφαιρικά; Μήπως και η Γη είναι ένα τεράστιο κουλούρι; Και αν είναι, θα μας το έλεγαν; ΤΟΙ ΜΑΣ ΚΡΕΙΒΟΥΝ αγαπητέ μου αναγνώστη;
Σου αρέσει η Καθημερινή Φυσική; Εγγράψου στο newsletter για να παίρνεις ειδοποίηση με κάθε νέα ανάρτηση (1-2 φορές τον μήνα). Μην ξεχάσεις το email επιβεβαίωσης!
Email:
Θέλεις να βοηθήσεις; Τέλεια! Πήγαινε στη σελίδα Υποστήριξη για να μάθεις πώς.
Δείτε το σχετικό βίντεο
Διαβάστε επίσης
Περισσότερες πληροφορίες
https://youtu.be/Aj6Kc1mvsdo (PBS Space Time - Why is the Earth round and the Milky Way flat?)
https://physics.aps.org/articles/v1/38 (The many shapes of spinning drops)
www.aleph.se/andart/archives/2014/02/torusearth.html (Can toroid planets exist?)

